Dong Zhou

EDUCATION

• Ph.D., Applied Mathematics, 2014. Temple University, Philadelphia, PA
• M.A., Mathematics, 2010. Temple University, Philadelphia, PA
• B.S., Mathematics, 2008. Beijing Normal University, Beijing, China

PROFESSIONAL APPOINTMENTS

• Assistant Professor, Department of Mathematics, California State University Los Angeles (August 2018 - present)
• Research Assistant Professor, Department of Mathematics, Temple University (August 2014 - July 2018)
• Visiting Scientist, Department of Mathematics, Massachusetts Institute of Technology (February 2015 - June 2015)

CURRENT TEACHING (FALL 2022)

• MATH 2110 Calculus
• MATH 4010 Ordinary Differential Equations

PAST TEACHING

• Fall 2021: MATH 2110 Calculus, MATH 5021 Applied Linear Analysis I
• Spring 2021: MATH 2110 Calculus I
• Fall 2020: MATH 2170 Computer Algebra Systems, MATH 5700 Numerical Linear Algebra
• Spring 2020: MATH 2111 Calculus I Workshop, MATH 5210 Mathematical Modeling, MATH 5710 Numerical Solutions of Partial Differential Equations
• Fall 2019: MATH 1040 PreCalculus, MATH 5700 Numerical Linear Algebra
• Spring 2019: MATH 1040 PreCalculus, MATH 5210 Mathematical Modeling
• Fall 2018: MATH 1040 PreCalculus, MATH 4700 Numerial Analysis

In many computational science and engineering applications, for example, fluid flow and interface propagation, it is extremely challenging to design numerical methods that achieve high order of accuracy. The main theme of my research is the development of numerical schemes that are high-order both in space and time, for partial differential equations arise in these applications.

Research Grant

National Science Foundation grant DMS-1719640. (August 2017 - July 2020)
Collaborative Research: Overcoming order reduction and stability restrictions in high-order time-stepping. Co-PI, with PI Benjamin Seibold (Temple University), and collaboration with Rodolfo Ruben Rosales (Massachusetts Institute of Technology), DMS-1719637, David Shirokoff (New Jersey Institute of Technology), DMS-1719693.

Unconditional Stability for Implicit-Explicit (ImEx) Multistep Methods

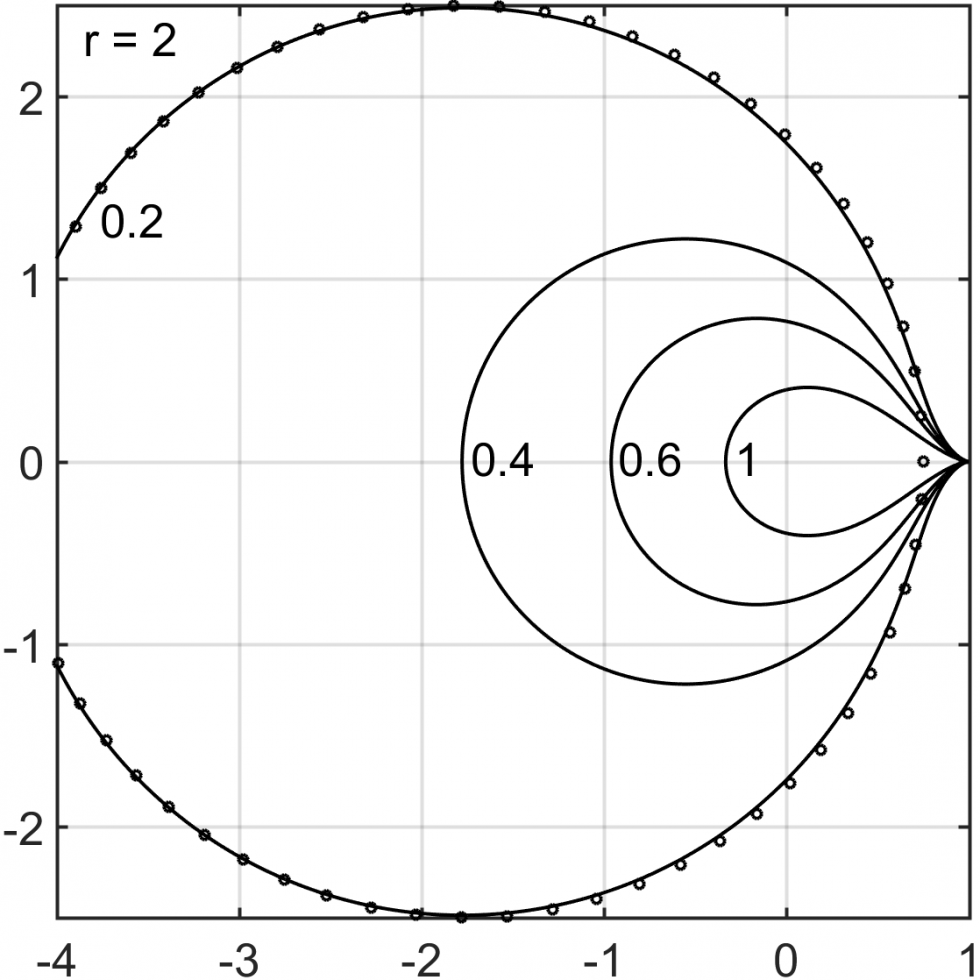
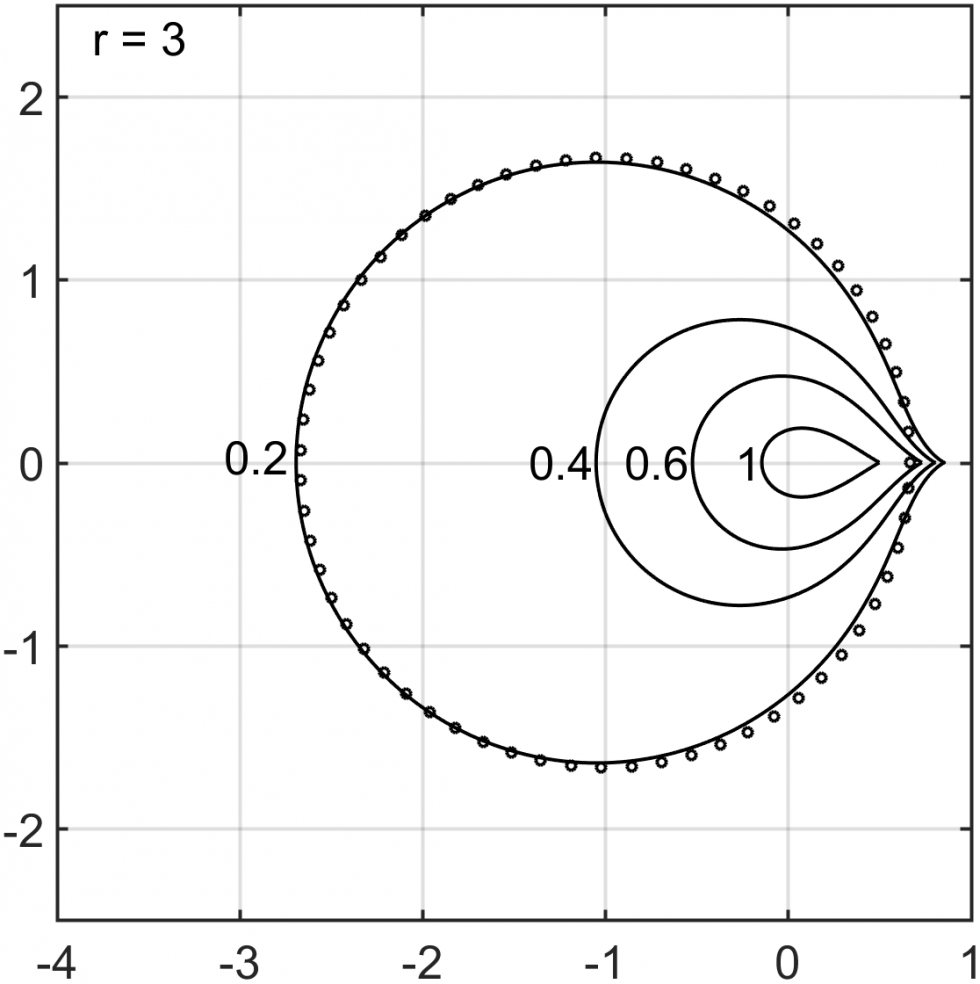
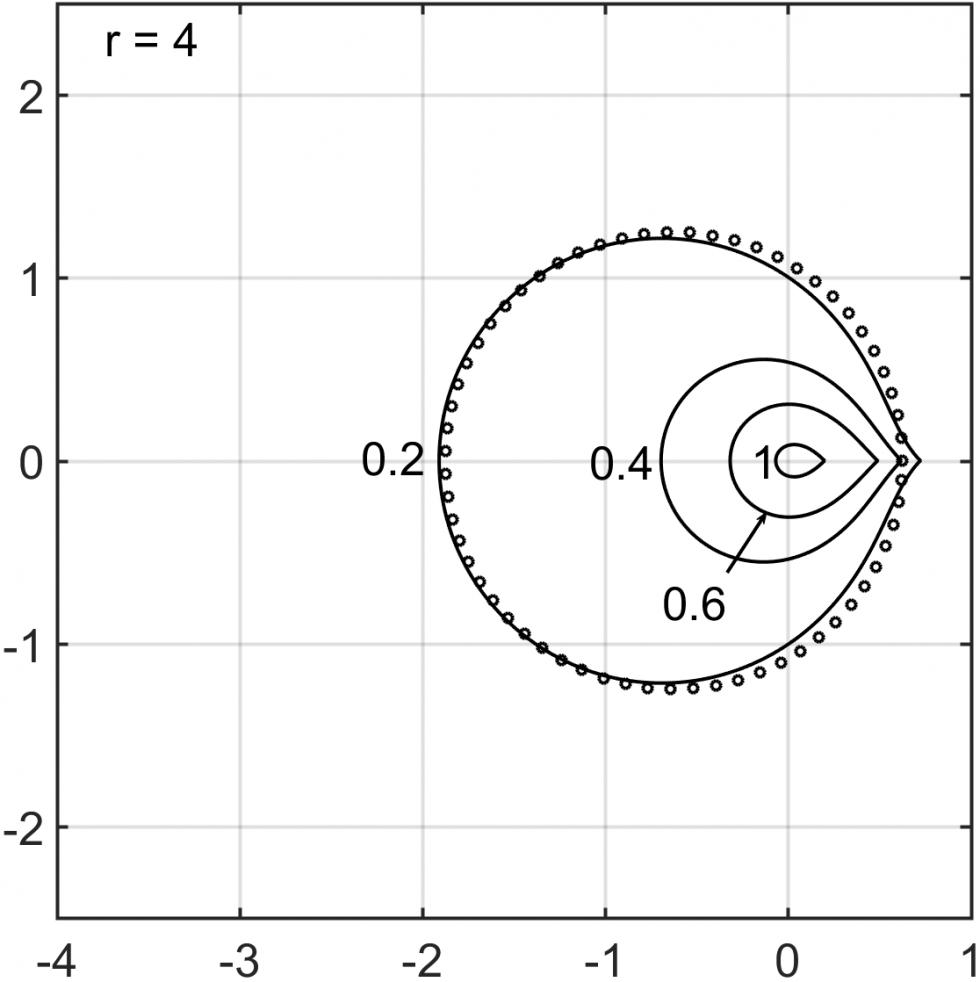
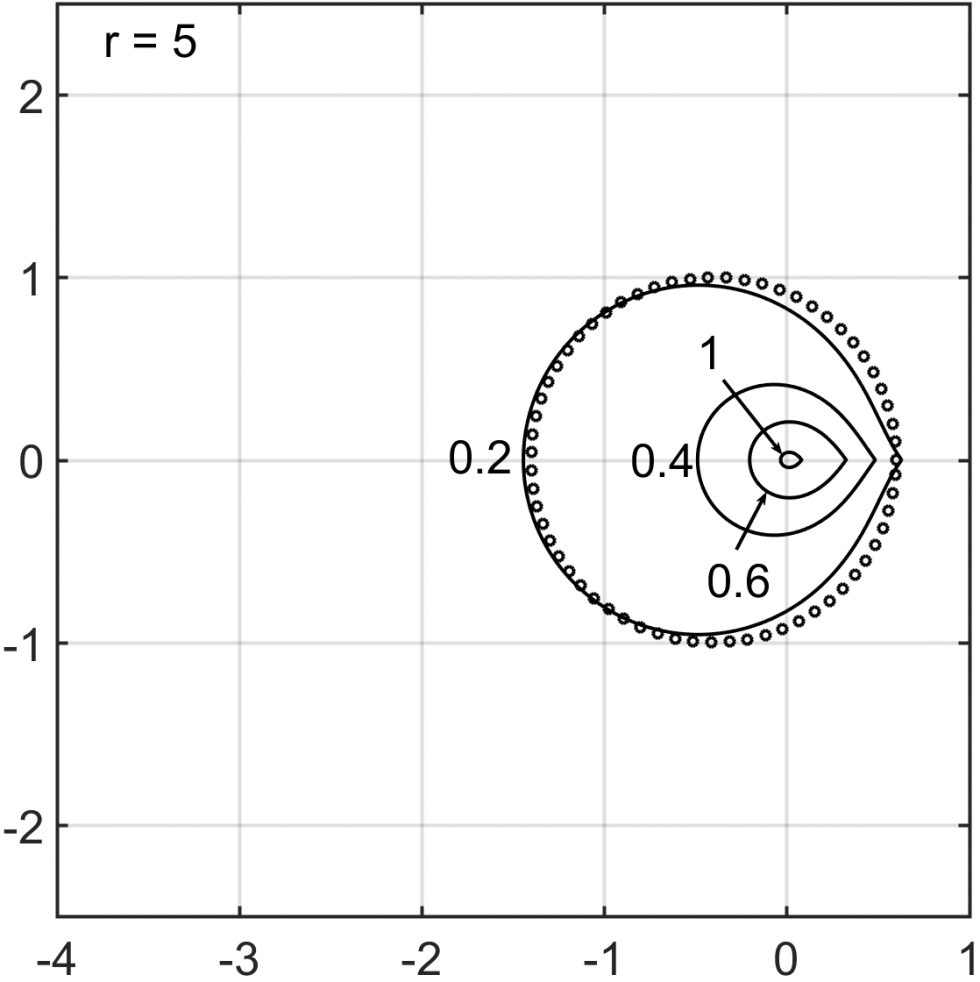
A fundamental drawback of high-order linear multistep methods is their restrictive stability properties compared to RK schemes. In this work, we develop a new stability theory that characterizes unconditional stability of ImEx multistep methods, and design a new class of ImEx multistep methods that possesses large regions of unconditional stability. Specifically, we consider ImEx multistep methods applied to a system of ordinary differential equations u_t=Au+Bu, where Au is treated implicitly and Bu is treated explicitly. We are particularly interested in the problem for which both A and B are stiff. Such splittings can arise, for example, in a pressure Poisson reformulations of the incompressible Navier-Stokes equations. Unconditional stability allows for time step selection solely based on accuracy consideration.

The new ImEx multistep methods have tunable parameters that control the size of the unconditional stability region, and can achieve unconditional stability for problems that are unstable with current popular schemes such as semi-implicit backward differentiation formulas (SBDF). Our new stability theory generalizes the existing stability theories, that make use of stability regions and matrix spectra of the problem, to ImEx multistep methods, and provides rigorous explanations for stability limitations in SBDF.

The figures above illustrate the unconditional stability regions for our new IMEX multistep methods from order 2 to 5, with different choice of the parameter δ. Note that δ=1 recovers SBDF methods.

Order Reduction in High-order Runge-Kutta Methods

Despite the advantages of locality in time and good stability properties, RK methods have a key drawback: in general they are affected by order reduction, meaning that the observed convergence order, when applied to stiff ODEs or initial boundary value problems (IBVP), is less than the formal order of the scheme.

In this work, we analyze the global errors incurred when applying an implicit RK scheme to a general IBVP u_t=Lu+f(x,t) with time dependent boundary conditions. We develop a theoretical framework that yields a fundamental geometric understanding of the mechanism for order reduction. Geometrically, the order reduction stems from the boundary layers, produced by the fact that the scheme is too accurate near the boundary (the approximation error satisfies a singularly perturbed boundary value problem). The amplitude of the boundary layers is limited by the stage order of the scheme, which in general less than the scheme’s order, thus order reduction.

Two remedies are developed to recover full convergence order:
(1) We derive a new condition, the weak stage order (WSO), for constructing new RK schemes devoid of order reduction. The novelty of this condition is that it is compatible with a diagonally implicit Runge-Kutta (DIRK) structure, in contrast to the high stage order which is impossible to achieve with DIRK schemes.
(2) The modified boundary conditions (MBC) achieve order reduction avoidance by suppressing the singular behavior in the numerical solutions computed from existing RK schemes. These boundary conditions are extracted via a formal power series expansion of the solution in the absence of the the singular behavior triggered by the conventional approach of enforcing boundary conditions.

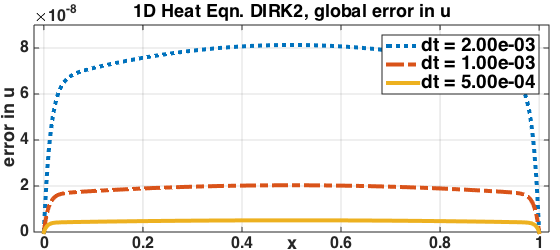
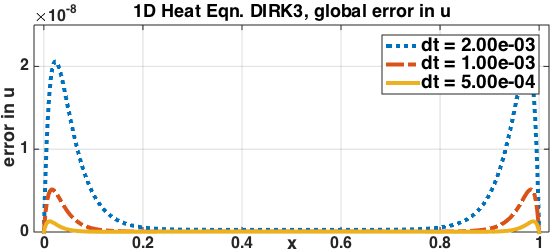
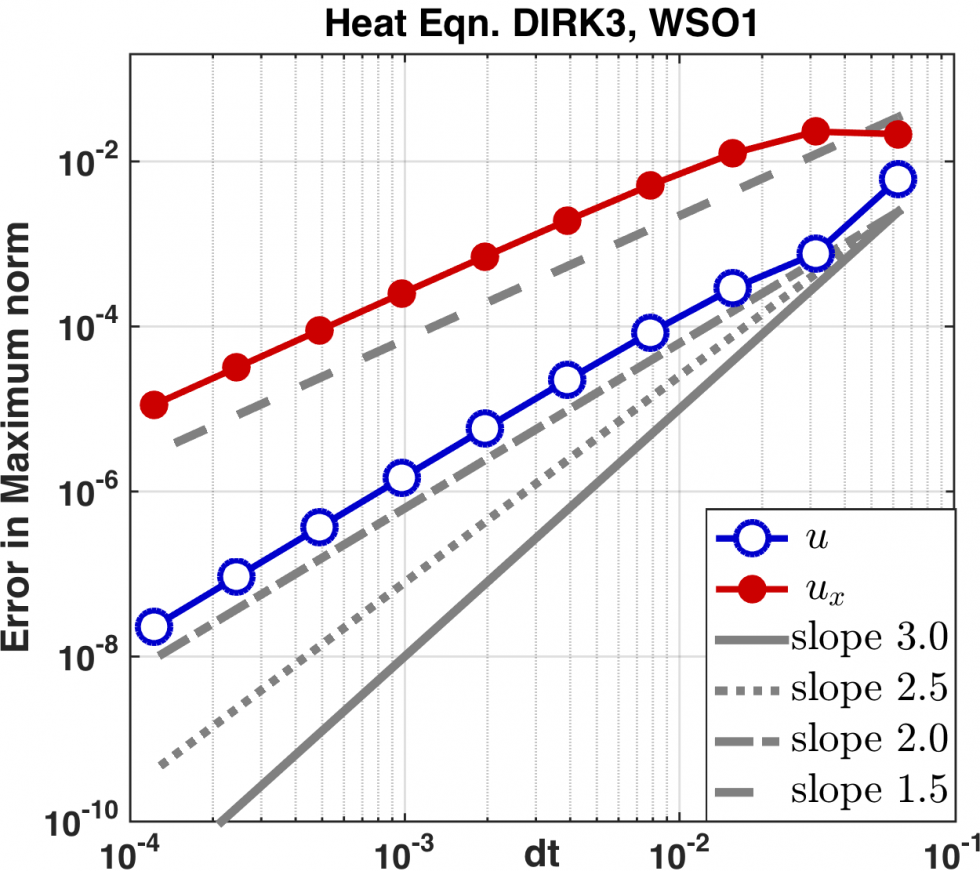
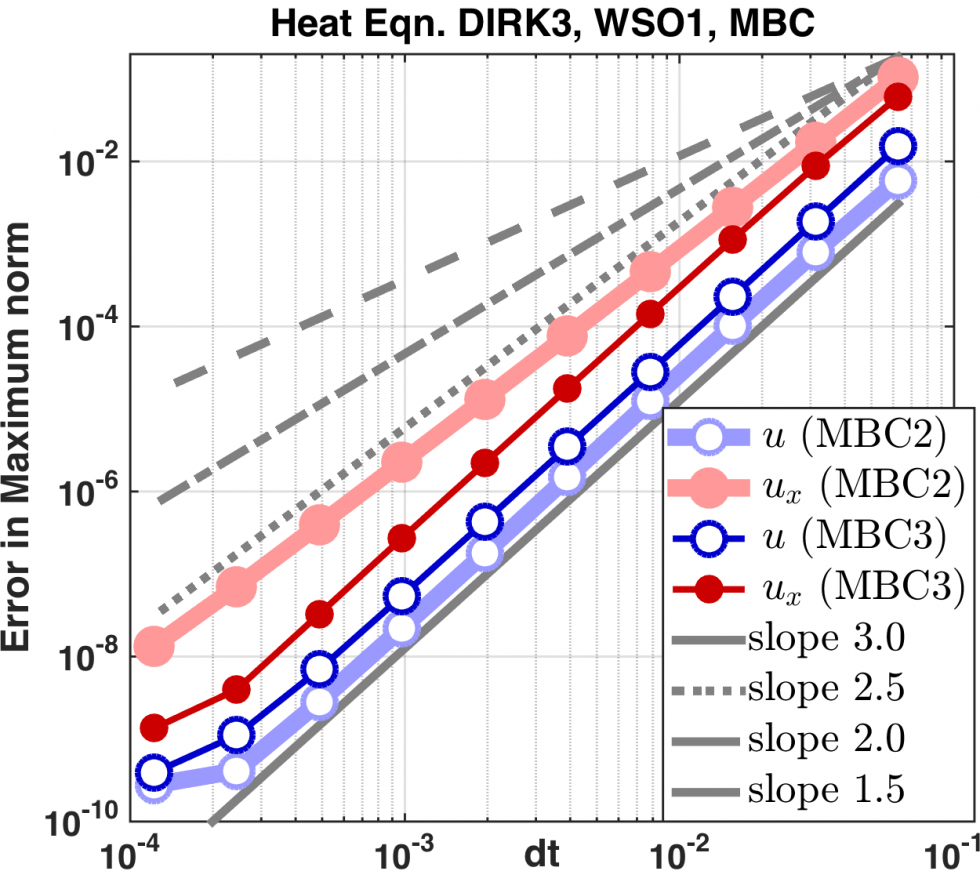
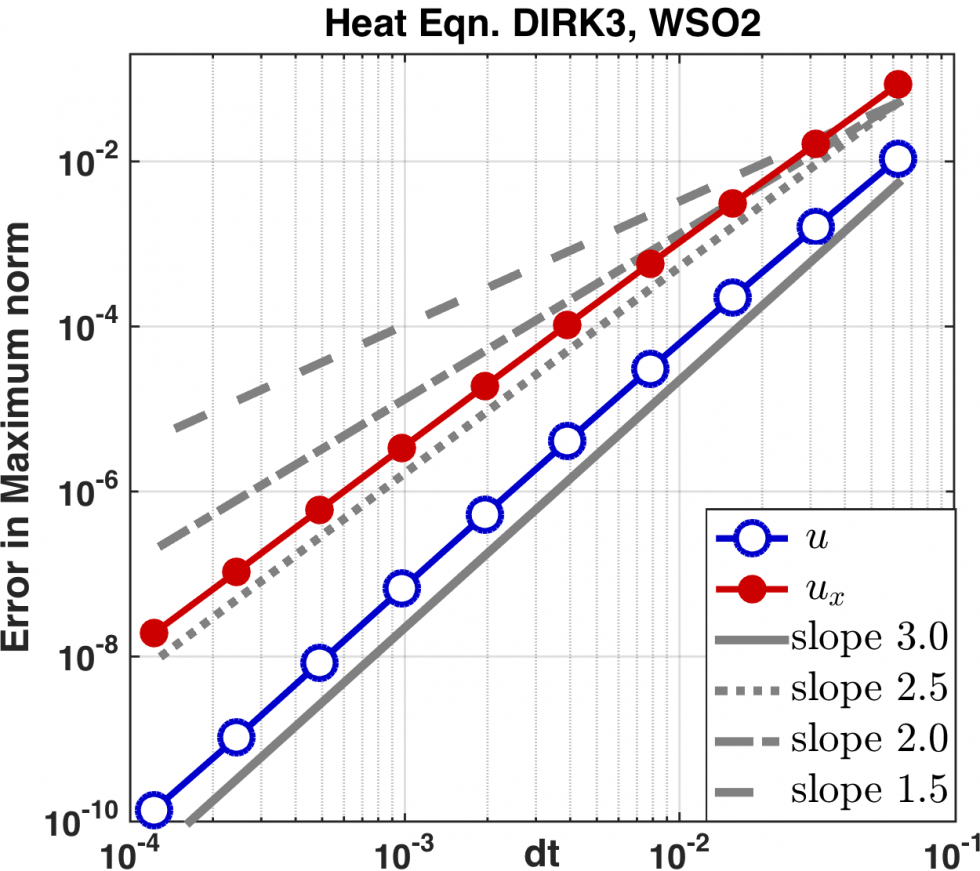
The figures above show the error convergence for 3rd order schemes for a 1D heat equation example. Left: 3rd order WSO 1 DIRK scheme with conventional b.c. exhibits order reduction. Middle: The same WSO 1 DIRK scheme with MBC recovers full 3rd order convergence in the function value u and the derivative u_x. Right: 3rd order WSO 2 DIRK scheme recovers 3rd order convergence in u.

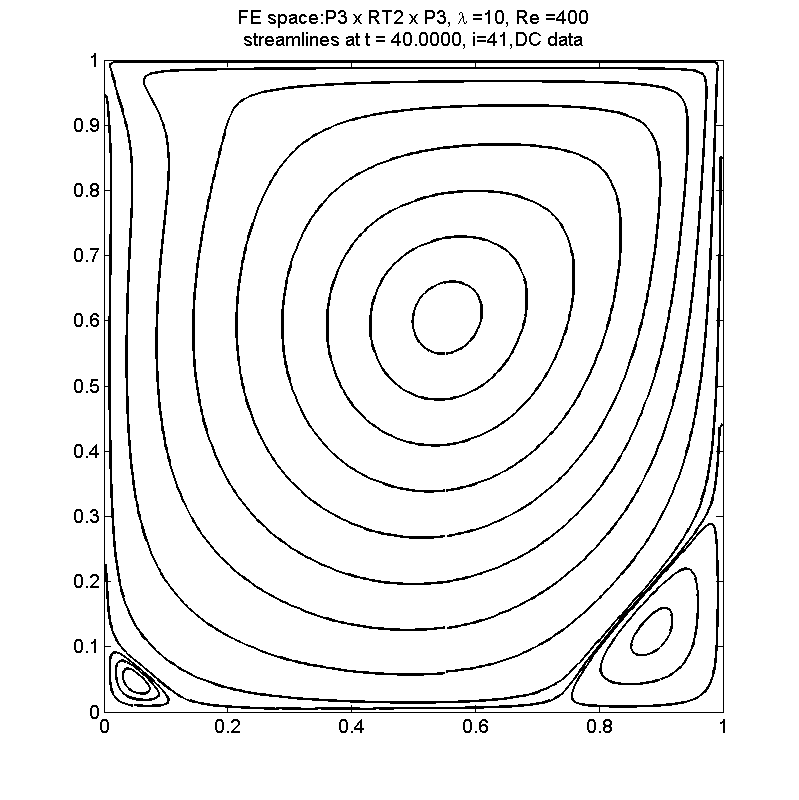
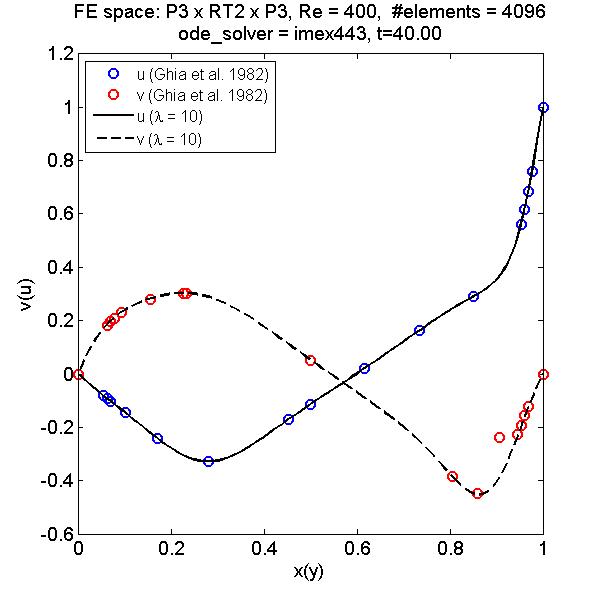
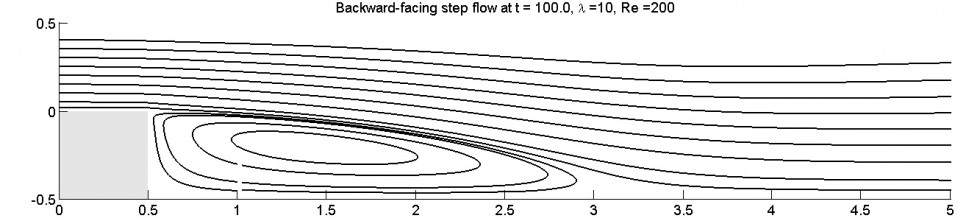
High-Order Methods for Incompressible Flow Problems

Pressure Poisson equation (PPE) reformulations of the incompressible Navier-Stokes equations is a class of methods that replace the incompressibility constraint by a Poisson equation for the pressure, with a proper choice of the boundary condition so that the incompressibility is maintained. This approach has important advantages compared to the standard form: (1) the pressure is not implicitly coupled to the velocity and can be recovered by solving a Poisson equation; (2) no numerical boundary layers are generated, in contrast to the projection type methods.

In this work, I proposed numerical methods for solving one PPE reformulation (Shirokoff and Rosales, 2011) using mixed finite element methods and meshfree finite differences in space with high-order implicit-explicit (ImEx) time-stepping in time. This PPE reformulation is special due to its electric boundary conditions (n×u=0 and ∇⋅u=0). The standard nodal-based FE approach will converge to the wrong solution on domains with reentrant corners or curved boundaries. The former is due to the insufficient regularity of the solution, and the latter is a form of Babuska paradox.

The mixed finite element approach is well-suited for electric boundary conditions, and the meshfree finite difference handles curved boundaries naturally. The ImEx Runge-Kutta methods are used to treat the viscous term implicitly and the pressure explicitly. The method achieves 3rd order convergence in time with a 3rd order IMEX RK method, for problems with time-independent boundary conditions and forcing at the boundary (a special case where order reduction does not occur).

JOURNAL PUBLICATIONS AND PEER-REVIEWED CONFERENCE PROCEEDINGS

• R. R. Rosales, B. Seibold, D. Shirokoff, D. Zhou. High-order finite element methods for a pressure Poisson equation reformulation of the Navier–Stokes equations with electric boundary conditions. Computer Methods in Applied Mechanics and Engineering, Vol. 373, 2021, pp. 113451. [doi] [arxiv]

• D. Ketcheson, B. Seibold, D. Shirokoff, D. Zhou. DIRK Schemes with High Weak Stage Order. In: Sherwin S., Moxey D., Peiró J., Vincent P., Schwab C. (eds) Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2018. Lecture Notes in Computational Science and Engineering, vol 134. Springer, Cham. [doi] [arxiv]

• B. Seibold, D. Shirokoff, D. Zhou. Unconditional Stability for Multistep ImEx Schemes: Practice. Journal of Computational Physics, Vol. 376, 2019, pp. 295-321. [doi] [arxiv]

• R. R. Rosales, B. Seibold, D. Shirokoff, D. Zhou. Unconditional Stability for Multistep ImEx Schemes: Theory. SIAM Journal on Numerical Analysis, Vol. 55, No. 5, 2017, pp. 2336-2360. [doi] [arxiv]

• D. Zhou, B. Seibold, D. Shirokoff, P. Chidyagwai, R. R. Rosales. Meshfree Finite Differences for Vector Poisson and Pressure Poisson Equations with Electric Boundary Conditions. In: Griebel, M. and Schweitzer, M. (eds) Meshfree Methods for Partial Differential Equations VII, Lecture Notes in Computational Science and Engineering, vol. 100. Springer, Cham, 2015, pp. 223-246. [doi] [arxiv]

PREPRINTS

• R. R. Rosales, B. Seibold, D. Shirokoff, D. Zhou. Spatial Manifestations of Order Reduction in Runge-Kutta Methods for Initial Boundary Value Problems. Preprint. [arxiv]